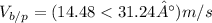Answer:
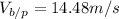 at an angle of 31.24°
at an angle of 31.24°
Step-by-step explanation:
We know that
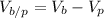 so we need the velocity of the ball relative to ground.
so we need the velocity of the ball relative to ground.
The equations for the ball in X and Y are these ones:

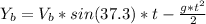
From X-axis equation:
 Replacing this value in the Y-axis equation we can find Vb:
Replacing this value in the Y-axis equation we can find Vb:
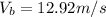 And this is the magnitude relative to ground. The components are:
And this is the magnitude relative to ground. The components are:
![V_(b)=[12.92*cos(37.3),12.92*sin(37.3)]=[10.28,7.83]m/s](https://img.qammunity.org/2020/formulas/physics/college/ijp3p7shcuqpxar3sdbsijyoauilprb2ma.png)
Now we calculate the velocity of the ball relative to the player as:
![V_(b/p) = V_(b)-V_(p)=[12.19,7.83]m/s](https://img.qammunity.org/2020/formulas/physics/college/3lo9b40mto8p9a4p71ptxn1juyzpavnufk.png) If we now calculate the magnitude and the angle of this vector, we get the answer to the problem:
If we now calculate the magnitude and the angle of this vector, we get the answer to the problem: