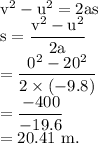Question

A ball is thrown vertically upward with a speed of 20 m/s. When will it reach the maximum height? What is the maximum height reached?

Answer 1

Time taken by the ball to reach maximum height = 2.041 seconds.

Maximum height that ball reached = 20.41 meters.

Step-by-step explanation:

Given that the initial speed of the ball,
`\rm u = 20\ m/s.`

We know, when the ball moves in upward direction, the acceleration due to gravity acts on it in downwards direction, therefore the affecting acceleration that acts on the ball
`\rm a = -g`.

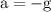g is the acceleration due to gravity having value
`\rm 9.8\ m/s^2`.

Also, the final speed of the ball at its maximum height will be 0, i.e.,
`\rm v=0\ m/s.`

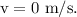
To find the time taken by ball to reach maximum height.

Let it reaches the maximum height in time t, using the following relation of Kinematics,

`\rm v=u+at\\0=20+(-9.8)t\\-20 = -9.8 t\\t=(-20)/(-9.8)=2.041\ s.`

To find the maximum height.

Let the maximum height upto ball goes be s, then using,

`\rm v^2-u^2=2as\\s=(v^2-u^2)/(2a)\\=(0^2-20^2)/(2* (-9.8))\\=(-400)/(-19.6)\\=20.41\ m.`

Answer 2

2.04 sec and 20.38 meters

Step-by-step explanation:

upward speed of the ball u = 20 m/s

final velocity of the ball v= 0 m/s

we know that
`v^2-u^2= 2gh`

`0^2- 20^2= 2* 9.81* h`

on solving we get

h= 20.38 meters. this the maximum height it will reach.

to calculate when it will reach maximum height

use u= gt

t= u/g

⇒ t= 20/9.81 = 2.04 sec after this much time it will reach to its maximum height.