Over what interval is the graph of f(x) = -(X + 8)2 - 1 decreasing? (-8,infinity) (8,infinity ) (-infinity ,8) (-infinity ,-8)

Question

asked Aug 2, 2020 71.7k views

2 Answers

Eleddy · Answer 1 · 2020-08-08T17:54:37+0000

Answer:

Function is decreasing on (-8,infinity)

Explanation:

The given function is
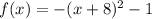
f(x)=-(x+8)^2-1

The first derivative is given by

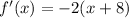
f'(x)=-2(x+8)

For the function to be decreasing, we have

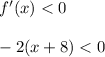
$f'(x)<0\\\\-2(x+8)<0$

Divide both sides by -2. Since, we are dividing by a negative number hence, the inequality sign will change.

(x+8)>0

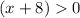
Subtract 8 to both sides

x>-8

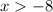
Therefore, the function is decreasing on (-8,infinity)

First option is correct.