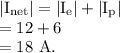Question

A certain cross section lies in the x–y plane. If 3 × 1020 electrons go through the cross section in the z direction in 4 seconds, and simultaneously 1.5 × 1020 protons go through the same cross section in the negative z direction, what is the magnitude and direction of the current flowing through the cross section?

Answer 1

The magnitude of the net current = 18 A.

Direction of the net current is along the negative z axis.

Step-by-step explanation:

Given:

• Number of electrons flow through the given cross section,
  `\rm n_e = 3* 10^(20)\ electrons.`
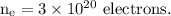
• Number of electrons flow through the given cross section,
  `\rm n_p = 1.5* 10^(20)\ protons.`
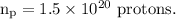
• Time interval for which the electrons and protons flow,
  `\rm t = 4\ seconds.`

The current through a cross section is defined as the amount of charge passing through that cross section in unit time.

`\rm I = (Q)/(t).`

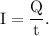
We know,

Charge on an electron,
`\rm q_e = -1.6* 10^(-19)\ C.`

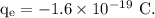
Charge on a proton,
`\rm q_p = +1.6* 10^(-19)\ C.`

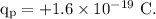
Therefore,

The amount of charge flowing due to electrons is given by

`\rm Q_e = n_eq_e=3* 10^(20)* -1.6* 10^(-19)=-48\ C.`

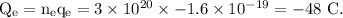
The amount of charge flowing due to protons is given by

`\rm Q_p = n_pq_p=1.5* 10^(20)* +1.6* 10^(-19)=+24\ C.`

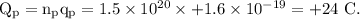
The current flowing through the cross section because of the electrons is given as:

`\rm I_e = (Q_e)/(t)=(-48\ C)/(4\ s)=-12\ A.`

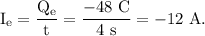
The negative sign shows that the current is due to the flow of negative charge, and the direction of current is always opposite to that of flow of negative charge i.e., electrons.

Thus, the direction of this current is along the negative z direction.

The magnitude of this current = 12 A.

The current flowing through the cross section because of the protons is given as:

`\rm I_p = (Q_p)/(t)=(+24\ C)/(4\ s)=6\ A.`

The direction of this current is same as that of electrons,

The directions of the currents due to both, the electrons and the protons are along the negative z direction, therefore the magnitude of the net current is given as:

`\rm |I_(net)| = |I_e|+|I_p|\\=12+6\\=18\ A.`