Question

A rock is projected upward from the surface of the Moon, at time t = 0 s, with an upward velocity of 30.0 m/s. The acceleration due to gravity at the surface of the Moon is 1.62 m/s2, and the Moon has no atmosphere. The height of the rock when it is descending with a speed of 20.0 m/s is closest to:

Answer 1

A rock is projected upwards from the surface of the moon at time t = 0.0 s with a velocity of 30 m/s (the acceleration due to gravity at the surface of the moon ...

Step-by-step explanation:

Answer 2

154.3 m

Step-by-step explanation:

We can solve this problem by using the law of conservation of energy.

In fact, the total mechanical energy of the rock at any point during the motion is the sum of the kinetic energy and the gravitational potential energy:

`E=(1)/(2)mv^2 + mgh`

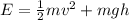
where

m is the mass of the rock

v is the speed

g = 1.62 m/s^2 is the acceleration of gravity on the Moon

h is the height

When the rock is launched upward, all the energy is just kinetic energy, so:

`E=(1)/(2)mu^2`

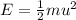
where

u = 30.0 m/s is the initial speed

Then at a certain height h while descending, its total energy is

`E=(1)/(2)mv^2 + mgh`

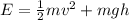
where

v = 20.0 m/s is the current speed

Since the total energy is conserved, we can write

`(1)/(2)mu^2 = (1)/(2)mv^2 + mgh`

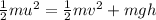
And re-arranging the equation, we can solve for h:

`h=(u^2-v^2)/(2g)=(30^2-20^2)/(2(1.62))=154.3 m`

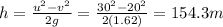
So, this is the height of the rock when it has a speed of 20.0 m/s.