Question

A particular automatic sprinkler system has two different types of activation devices for each 3 sprinkler head. One type has a reliability of 0.9; that is, the probability that it will activate the sprinkler when it should is 0.9. The other type, which operates independently of the first type, has a reliability of 0.8. If either device is triggered, the sprinkler will activate. Suppose a fire starts near a sprinkler head. What is the probability that the sprinkler head will be activated?

Answer 1

There is an 85% probability that the sprinkler head will be activated.

Explanation:

We have these following probabilities:

50% of the first sprinkler being triggered

90% of the first sprinkler being reliable

50% of the second sprinkler being triggered

80% of the second sprinkler being reliable.

What is the probability that the sprinkler head will be activated?

`P = P_(1) + P_(2)`

`P_(1)` is the probability of the first sprinkler being triggered and activated. So:

`P_(1) = 0.5*0.9 = 0.45`

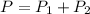
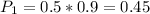
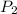`P_(2)` is the probability of the second sprinkler being triggered and activated. So:

`P_(2) = 0.5*0.8 = 0.40`

`P = P_(1) + P_(2) = 0.40 + 0.45 = 0.85`

There is an 85% probability that the sprinkler head will be activated.