Question

How do you find the sum of the first 25 terms in a sequence?

Answer 1

Explanation:

It's very necessary to find whether the given sequence is arithmetic or geometric.

In Arithmetic sequence every successive term has a common difference and in geometric sequence every successive term shows a common ratio.

Example of Arithmetic sequence:

1, 2, 3, 4, 5......

2 - 1 = 1

3 - 2 = 1

common difference of 1.

Example of geometric sequence:

2, 4, 8, 16..........

`(4)/(2)=2`

`(8)/(4)=2`

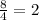
Common ratio of 2

Now formula to calculate the sum of initial n terms of Arithmetic sequence

`S_(n)=(n)/(2)[2a+(n-1)d]`

where a = first term

n = number of terms to be added

d = common difference

Formula to calculate the sum of initial n terms of the Geometric sequence

`S_(n)=(a(r^(n) -1))/(r-1)`

where a = first term of the sequence

n = number of terms to be added

r = common ratio

With help of these formula we can find the sum of first 25 terms of any sequence given.

Answer 2

Hey!

-----------------------------------------------

Explanation and Answer:

Find the difference between 2 points and see if the sequence is proportional. Then just keep adding till you get to the 25th sequence.

Let's say the sequence is 3,5,7,9,11. We subtract 2 points and we get 2. Each number is +3. After adding we get 50 as the 25th term.

-----------------------------------------------

Hope This Helped! Good Luck!