Question

The indicator dilution method is a technique used to determine flow rates of fluids in channels for which devices like rotameters and orifice meters cannot be used. A stream of an easily measured substance (the tracer) is injected into the channel at a known rate and the tracer concentration is measured at a point far enough downstream of the injection point for the tracer to be completely mixed with the flowing fluid. The larger the flow rate of the fluid, the lower the tracer concentration at the measurement point.A gas stream that contains 1.50 mole% CO2 flows through a pipeline. 20.0 kg/min of CO2 is injected into the line. A sample of the gas is drawn from a point in the line 10 meters downstream of the injection point and found to contain 2.3 mole% CO2.1) Estimate the gas flow rate (kmol/min) upstream of the injection point.2) Eighteen seconds elapses from the instant the additional CO2 is first injected to the time the CO2 concentration at the measurement point begins to rise. Assuming that the tracer travels at the average velocity of the gas in the pipeline (i.e. neglecting diffusion of CO2), estimate the average velocity (m/s). If the molar gas density is 0.123 kmol/m3, what is the pipe diameter?

Answer 1

1) 19.739 kmol/min

2) v = 0.021 m/s

D = 12.788 m

Step-by-step explanation:

1) By the mass balance, the amount that enters a system such be the amount the goes out, if there isn't accumulation.

Knowing that the molar masses are: C = 12 kg/kmol and O = 16 kg/kmol; CO₂ has molar mass equal to: 12 +2x16 = 44 kg/kmol. So, the initial flow rate of CO₂ is

`(20 kg/min)/(44 kg/kmol) = 0.454 kmol/min`

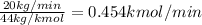
Which is the same of the upstream. So, if the concentration of CO₂ is 2.3 % or 0.023, than the flow rate of the gas(F) will be:

0.023F = 0.454

F = 19.739 kmol/min

2) First, let's estimate the velocity of the gas. The pipeline has 10 meters, and the flow occurs during 8 min = 480 s, so the velocity is:

v = 10/480 = 0.021 m/s

For a flow of 19.739 kmol/min during 8 min, the number of moles of the gas will be:

n = 19.739x8 =157.912 kmol

The density is the number of moles divided by the volume, so:

0.123 = 157.912/V

V = 157.912/0.123

V = 1283.837 m³

The pipeline is a cylinder, so the volume is:

V = πxr²xH

Where π = 3.14, r is the radius and H the height of the pipeline = 10 m

1283.837 = 3.14xr²x10

r² = 40.886

r = √40.866

r = 6.394 m

The diameter is two radius, so

D = 12.788 m