Question

It takes a person 60 minutes to get to campus. He spends t minutes walking to the bus stop and the rest of the time riding the bus. His walking rate is 0.06 miles per minute and the bus travels at a rate of 0.5 miles per minute. The total distance walking and traveling by bus is given by the algebraic expression 0.06 t plus 0.5 left parenthesis 60 minus t right parenthesis. ​(a) Simplify the algebraic expression. ​(b) Use each form of the algebraic expression to determine the total distance that the person travels if the person spends 20 minutes walking to the bus stop.

Answer 1

a)
`S(t) = 30 - 0.44t`

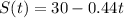
b) The person travels 21 miles

Explanation:

(a) Simplify the algebraic expression:

About the algebraic expression, the problem states that:

The total distance walking and traveling by bus is given by the algebraic expression 0.06 t plus 0.5 left parenthesis 60 minus t right parenthesis.

Mathematically, this is:

`S(t) = 0.06t + 0.5*(60-t)`.

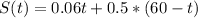Simplifying, we have:

`S(t) = 0.06t + 30 - 0.5t`

`S(t) = 30 - 0.44t`

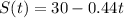
b) Use each form of the algebraic expression to determine the total distance that the person travels if the person spends 20 minutes walking to the bus stop.

t is the time that the person spends walking to the bus stop, so
`t = 20`.

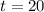By the original expression

`S(t) = 0.06t + 0.5*(60-t)`

`S(20) = 0.0620 + 0.5*(60-20) = 1.2 = 20 = 21.2`

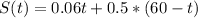
By the simplified expression

`S(t) = 30 - 0.44t`

`S(20) = 30 - 0.44*(20) = 30 - 8.8 = 21.2`

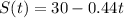
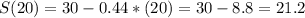
By each form of the expression, we find that the person traveled 21.2 miles