Answer:
First question: Since this shape is a square, the midpoint of the two diagonals shall coincide with each other.
Second question: assume that by "midpoint" the question refers to the centroid of the triangle. The centroid of a triangle is on its median 2/3 the way from the corresponding vertice.
Explanation:
First question
Midpoint of the diagonal between (x1, y1) and (x3, y3):
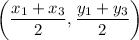 .
.
Similarly, midpoint of the diagonal between (x2, y2) and (x4, y4):
 .
.
The two midpoints shall coincide. Therefore,
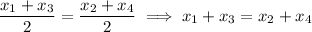 .
.
Similarly,
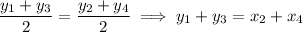 .
.
Second question
The centroid of a triangle divides all three of its medians at a 2:1 ratio. If the length of a median of the triangle is
 , the centroid of that triangle is at a distance of
, the centroid of that triangle is at a distance of
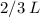 from the vertex on that median.
from the vertex on that median.
Start with the median that goes through the vertex
 . That median also goes through the midpoint between
. That median also goes through the midpoint between
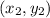 and
and
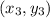 .
.
- Vertex:
 .
. - Midpoint of the opposite side:
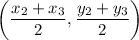
The centroid will be located at
![\displaystyle \left (\phantom{\frac{\phantom{x_(1)}}{2}}\right.x_1 + (2)/(3)\underbrace{\left((x_2 + x_3)/(2) - x_1\right)}_{\begin{gathered}\text{Separation}\\[-0.5em]\text{in }x\text{-}\\[-0.5em]\text{direction}\end{gathered}}, \quad y_1 + (2)/(3)\underbrace{\left((y_2 + y_3)/(2) - y_1\right)}_{{\begin{gathered}\text{Separation}\\[-0.5em]\text{in }y\text{-}\\[-0.5em]\text{direction}\end{gathered}}}\left.\phantom{\frac{\phantom{x_(1)}}{2}}\right)\right)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/uryz5e0gyy3f9rvg6ue0e4atayen06vwz3.png) .
.
Simplify this expression to obtain:
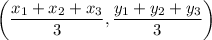 .
.