Answer:
819.78 m
Step-by-step explanation:
Given:
- OA = range of initial position of the airplane from the point of observation = 375 m
- OB = range of the final position of the airplane from the point of observation = 797 m
 = angle of the initial position vector from the observation point =
= angle of the initial position vector from the observation point =
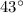
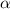 = angle of the final position vector from the observation point =
= angle of the final position vector from the observation point =
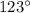
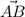 = displacement vector from initial position to the final position
= displacement vector from initial position to the final position
A diagram has been attached with the solution in order to clearly show the position of the plane.
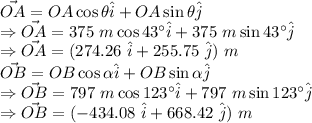
Displacement vector of the airplane will be the shortest line joining the initial position of the airplane to the final position of the airplane which is given by:
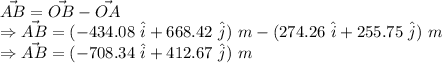
The magnitude of the displacement vector =
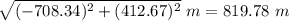
Hence, the magnitude of the displacement of the plane is 819.67 m during the period of observation.