Question

Suppose that the prevalence of a disease in a population is 0.1%, that is, 1 out of 1000 people in the population have the disease. A diagnostic test for this disease indicates its presence 99% of the times when it is actually present and 2% of the times when it is not. What is the probability that a randomly selected person from the population does not have the disease if the above diagnosis indicates that he/she has it? Comment on your answer.

Answer 1

Probability that person does not have disease when test is positive=0.9527

Explanation:

Given,

Probability of a person having disease,

`P(A)\ =\ (1)/(1000)`

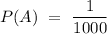
= 0.001

Then,probability of a person not having disease,

`P'(A)\ =\ 1\ -\ (1)/(1000)`

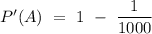
= 1 - 0.001

= 0.999

Probability that the test shows positive when disease is present,

`P(B/A)\ =\ (99)/(100)`

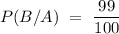
Then, probability that the test shows negative when disease is present,

`P(B'/A)\ =\ 1\ -\ (99)/(100)`

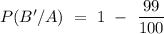
= 1 - 0.99

= 0.01

Probability that test will positive when disease will not present,

`P(B/A')\ =\ (2)/(100)`

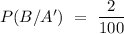
= 0.02

Then, probability that the test will be negative when disease will not present,

`P(B'/A')\ =\ 1\ -\ (2)/(100)`

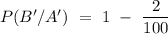
= 0.98

Then, the probability that the test will be positive either the disease will present or not,

P(B) = P(B/A).P(A) + P(B/A').P(A')

= 0.99 x 0.001 + 0.02 x 0.999

= 0.02097

Then, the probability that person does not have disease when test is positive,

`P(A'/B)\ =\ (P(B/A')* P(A'))/(P(B))`

`=\ (0.02* 0.999)/(0.02097)`

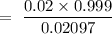
= 0.9527

Hence,the probability that person does not have disease when test is positive = 0.9527