Answer:
a)
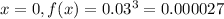
b)
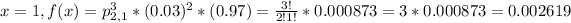
c)
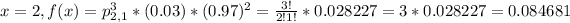

Explanation:
The problem states that there is a 97% probability that a parts inspected is classified correctly. So, there is a 3% probability that a part inspected is not classified correctly.
So
(A) x = 0, f(x) = ?
What is the probability that each part is not classified correctly?

There is a 0.0027% probability that no part is classified correctly
(B) x = 1, f(x) = ?
What is the probability that exactly one part is classified correctly?
We have to take into account that it may be the first part classified correctly, the second or the third. So we have to permutate. We have a permutation of 3 parts with 1(classified correctly) and 2(classified incorrectly) repetitions.
So
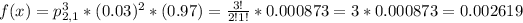
There is a 0.2619% probability that no part is classified correctly.
(C) x = 2, f(x) = ?
What is the probability that exactly two parts are classified correctly?
We also have the permutation of 3 parts with 2 and 1 repetitions.
So:
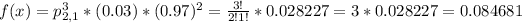
There is a 8.4681% probability that exactly two parts are classified correctly.
(D) x = 3, f(x) = ?
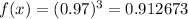
There is a 91.2673% probability that every part is classified correctly