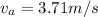Answer:
Part a)
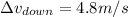
Part b)
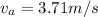
Step-by-step explanation:
Since ball is dropped under uniform gravity
so here we can say that the distance of 3 m moved by the ball under uniform acceleration is given as
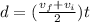
so we have
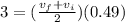
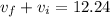
also we know that
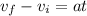
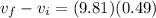
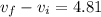
now we will have
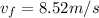
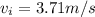
Part a)
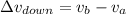
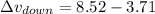
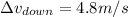
Part b)
speed at the top of the window is