Question

1. A robber drops a bag of loot into a 30 m well. If the speed of sound is 340 m/s, how long after dropping the bag does he hear the splash? [2.56 sec] 2. A penny is dropped off a tall building and hits the ground 5 seconds later. How tall is the building? 3. A diver falls from a 10m tower. How fast is she moving when she hits the water? [- 14 m/s] 4. A basketball player has a maximum vertical jump of 0.72 m. What is his speed when he leaves the floor? 5. A stone is thrown down a hole with a speed of 3 m/s and hits the bottom 1.8 sec later. a. How deep is the hole? [21.3 m] b. How fast is the stone traveling when it hits? [-20.61m/s] 6. .A juggler throws a ball upward and catches it 3.5 seconds later. a. What is the ball’s initial velocity? b. What is the ball’s maximum height? c. Sketch the displacement, velocity, and acceleration versus time graphs 7. A young vandal wishes to hit a truck traveling at a constant speed of 20m/s with a water balloon . If the vandal is in a tree, 40 m from the top of the truck, how far should the truck be from the tree when she releases the balloon so that it hits the truck when it is at a position directly beneath her? [57 m]

Answer 1

1. 2.56 s

First of all, we need to calculate the time it takes for the bag to fall down and reach the bottom of the well; this can be done by using the equation

`d=(1)/(2)at^2`

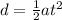
where

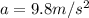`a=9.8 m/s^2` is the acceleration of gravity

t is the time

We now that the distance covered is d = 30 m, so we can solve for t:

`t_1=\sqrt{(2d)/(a)}=\sqrt{(2(30))/(9.8)}=2.47 s`

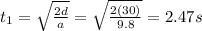
Now we also have to calculate the time it takes for the sound to cover the 30 m and reach the robber, which is:

`t_2 = (d)/(v)=(30)/(340)=0.09 s`

So, the robber will hear the splash after a total time of

`t=t_1 +t_2 = 2.47+0.09 = 2.56 s`

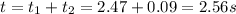
2. 122.5 m

For this problem, we can use again the following equation:

`d=(1)/(2)at^2`

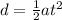
where

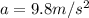`a=9.8 m/s^2` is the acceleration of gravity

t is the time

Here we know that the total time of the fall of the penny is

t = 5 s

So, the distance covered by the penny (which is equal to the heigth of the building) is

`d=(1)/(2)(9.8)(5)^2=122.5 m`

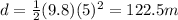
3. -14 m/s

For this problem, we can use the following equation:

`v^2 - u^2 = 2ad`

where

v is the final velocity

u = 0 is the initial velocity

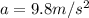`a=9.8 m/s^2` is the acceleration of gravity

d = 10 m is the distance covered (the height of the tower)

Solving for v,

`v=√(2ad)=√(2(9.8)(10))=14 m/s`

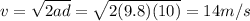
And since the velocity points downward, we can write it as -14 m/s.

4. 3.76 m/s

We can solve this problem by using the equation

`v^2-u^2=2ad`

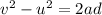
where:

v is the speed of the player at its point of maximum height

u is his speed as he leaves the floor

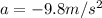`a=-9.8 m/s^2` is the acceleration of gravity (we take it negative as we consider upward as positive direction)

d = 0.72 m is the maximum height reached above the floor

At the point of maximum height, the velocity is zero: v = 0. Therefore, we can solve the formula for u, the initial speed:

`u=√(2ad)=√(2(-9.8)(0.72))=3.76 m/s`

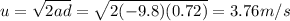
5. 21.3 m, -20.6 m/s

a) Taking downward as positive direction, we can use the equation

`d=ut+(1)/(2)at^2`

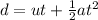
where

u = 3 m/s is the initial velocity

t = 1.8 s is the time

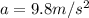`a=9.8 m/s^2` is the acceleration of gravity

Substituting, we find d, the depth of the hole:

`d=(3)(1.8)+(1)/(2)(9.8)(1.8)^2=21.3 m`

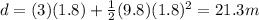
b)

The velocity of the stone at time t is given by

`v=u+at`

Substituting,

`v=3+(9.8)(1.8)=20.6 m/s`

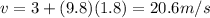
And if we consider upward as positive direction, this becomes -20.6 m/s.

6. 17.2 m/s, 15.1 m, see attachment for the graphs

a. The time taken for the ball to reach the maximum heigth is half the total time:

`t=(3.5)/(2)=1.75 s`

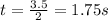
We can now use the equation

`v=u+at`

where

v = 0 is the velocity at the maximum height

u is the initial velocity

t = 1.75 s is the time

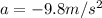`a=-9.8 m/s^2` is the acceleration of gravity

Solving for u,

`u=v-at=0-(-9.8)(1.75)=17.2 m/s`

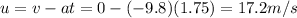
b.

We can calculate the maximum height using

`v^2-u^2=2ad`

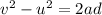
Solving for d,

`d=(v^2-u^2)/(2a)=(0^2-(17.2)^2)/(2(-9.8))=15.1 m`

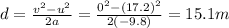
c. See attachments

The displacement increases as the ball goes higher until it reaches its maximum height (15.1 m), then it decreases until the ball reaches again the position d=0.

The velocity is obtained by computing the slope of the displacement-time graph. Its initial value is 17.2 m/s, then it decreases constantly until it reaches zero (point of maximum height), then it becomes negative and continues decreasing (increasing in magnitude, as the ball accelerates downward)

The acceleration is obtained from the slope of the velocity-time graph. Since the motion of the ball is free fall, the acceleration is constant and equal to -9.8 m/s^2.

7. 57.2 m

The time it takes the balloon to fall to the ground is given by:

`d=(1)/(2)at^2`

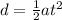
where

d = 40 m is the heigth

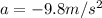`a=-9.8 m/s^2` is the acceleration of gravity

Solving for t,

`t=\sqrt{(2d)/(a)}=\sqrt{(2(40))/(9.8)}=2.86 s`

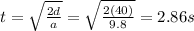
The distance covered by the truck during this time is

`d=vt`

where v = 20 m/s is the speed of the truck. Substituting,

`d=(20)(2.86)=57.2 m`

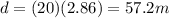
Therefore, the truck must be 57.2 m far when the vandal drops the balloon.