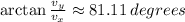Question

In a local bar, a customer slides an empty beer mug down the counter for a refill. The height of the counter is 1.28 m. The mug slides off the counter and strikes the floor 0.40 m from the base of the counter. (a) With what velocity did the mug leave the counter? Does the time required for the mug to hit the floor depend on its initial horizontal velocity? m/s (b) What was the direction of the mug's velocity just before it hit the floor? You appear to have correctly calculated the angle using your incorrect value from part (a).° (below the horizontal)

Answer 1

a) 0.78 m/s

b)The velocity vector points 81.1 degrees with respect to the horizontal

Step-by-step explanation:

First of all we need to figure the air time of the mug. It will fall from an initial height of 1.28 m without vertical initial speed thus
`v_(0y)=0 \, m/s`.

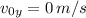The vertical displacement equation is given by:

`y(t)=-(1)/(2)gt^2+v_(0y)t+y_0=-(1)/(2)gt^2+1.28`

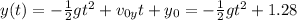
Plugging in the values of
`y_0=1.28\, m`,
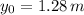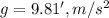`g=9.81 ', m/s^2` and
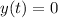`y(t)=0` (because we want to know at what time
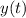`y(t)` equals zero, that is the position of the mug is at the floor) we get the following equation:

`0=-(1)/(2)gt^2+y_0\implies t=\sqrt(2y_0)/(g)`

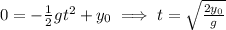
For the x and y velocities we have:

`v_x=v_(0x)=(d_x)/(t)=\frac{0.40}{\sqrt{(2y_0)/(g)}}\approx 0.78\, m/s`

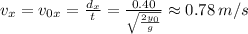
The above gives the first answer, let's continue with the y velocity:

`v_y=-gt`

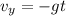
For the y-velocity at the instant the mug is in the floor we have:

`v_y=-gt\approx -5\, m/s`

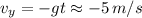
To know the angle of direction of the velocity vector with respect to the horizontal we have:

`\arctan{(v_y)/(v_x)\approx 81.11 \, degrees`