Question

Julie throws a ball to her friend Sarah. The ball leaves Julie's hand a distance 1.5 meters above the ground with an initial speed of 16 m/s at an angle 28 degrees; with respect to the horizontal. Sarah catches the ball 1.5 meters above the ground. 1) What is the horizontal component of the ball’s velocity right before Sarah catches it?

Answer 1

14.13 m/s

Step-by-step explanation:

This is the example of projectile motion. In case of projectile motion, the acceleration in horizontal direction is always zero as no external force is acting in this direction. So, the component of velocity along horizontal direction remains constant throughout the motion.

Thus, the horizontal component of velocity = u cos 28

= 16 cos 28 = 14.13 m/s

Answer 2

(1) 14.12 m/s

Step-by-step explanation:

Given:

• 
  `u` = initial speed of the ball = 16 m/s
• 
  `\theta` = angle of the initial speed with the horizontal axis =
  `28^\circ`
• 
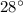
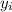  `y_i` = initial height of the ball from where Julie throws the ball = 1.5 m
• 
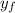  `y_f` = final position of the ball where Sarah catches the ball = 1.5 m

Let us assume the following:

• 
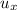  `u_x` = horizontal component of the initial speed
• 
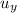  `u_y` = vertical component of the initial speed
• 
  `a_x` = horizontal acceleration of the ball
• 
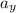  `a_y` = vertical acceleration of the ball

The given problem is projectile motion. When the ball is thrown from the air with a speed of 16 m/s at an angle 28 degree with the horizontal axis. When the ball is in the air, it experiences an only gravitational force in the downward direction if we ignore air resistance on the ball.

This means if we break the motion of the ball along two axes and study it, we have a uniform acceleration motion in the vertical direction and a zero acceleration motion along the horizontal.

Since the ball has a zero acceleration motion along the horizontal axis, the ball must have a constant speed along the horizontal at all instant of time.

Let us find out the initial velocity horizontal component of the velocity of the ball. which is given by:

`u_x = u\cos 28^\circ = 16* \cos 28^\circ = 14.12\ m/s`

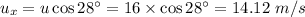
As this horizontal velocity remains constant in the horizontal motion at all instants of time. So, the horizontal component of the ball's velocity when Sarah catches the ball is 14.12 m/s.

Hence, the horizontal component of the ball's velocity when the ball is caught by Sarah is 14.12 m/s.