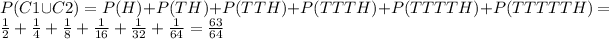Question

A coin is to be tossed as many times as necessary to turn up one head. Thus the elements c of the sample space C are H, TH, TTH, TTTH, and so forth. Let the probability set function P assign to these elements the respective probabilities 1 2 , 1 4 , 1 8 , 1 16 , and so forth. Show that P(C) = 1. Let C1 = {c : c is H,TH,TTH,TTTH, or TTTTH}. Compute P(C1). Next, suppose that C2 = {c : c is TTTTH or TTTTTH}. Compute P(C2), P(C1 ∩ C2), and P(C1 ∪ C2).

Answer 1

Explanation:

As stated in the question, the probability to toss a coin and turn up heads in the first try is
`(1)/(2)`, in the second is
`(1)/(4)`, in the third is
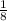`(1)/(8)` and so on. Then, P(C) is given by the next sum:

`P(C)=\sum^(\infty)_(n=1)((1)/(2) )^(n)=1`

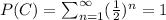
This is a geometric series with factor
`(1)/(2)`. Then is convergent to
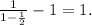`(1)/(1-(1)/(2))-1=1.`. With this we have proved that P(C)=1.

Now, observe that

`P(H)=(1)/(2), P(TH)=(1)/(4),P(TTH)=(1)/(8),P(TTTH)=(1)/(16),P(TTTTH)=(1)/(32),P(TTTTTH)=(1)/(64).`

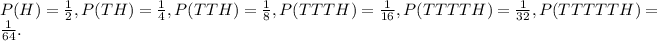
Then

`P(C1)=P(H)+P(TH)+P(TTH)+P(TTTH)+P(TTTTH)=(1)/(2) +(1)/(4) +(1)/(8) +(1)/(16) +(1)/(32) =(31)/(32)`

`P(C2)=P(TTTTH)+P(TTTTTH)=(1)/(32)+(1)/(64) =(3)/(64)`

`P(C1\cap C2)=P(TTTTH)=(1)/(32)`

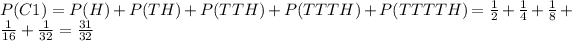
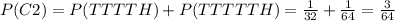
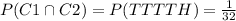
and

`P(C1\cup C2)=P(H)+P(TH)+P(TTH)+P(TTTH)+P(TTTTH)+P(TTTTTH)=(1)/(2) +(1)/(4) +(1)/(8) +(1)/(16) +(1)/(32) +(1)/(64)=(63)/(64)`