Question

infinite cylindrical rod of radius, R, oriented along the z-axis has both a volume charge density, rho = rho0 s R, that only depends on the radial distance, s, and a surface charge, λ = λ0, so that the entire rod is electrically neutral. Note: s, ϕ and z are the coordinates in the cylindrical coordinate system. (a) Determine the magnitude and direction of the electric field in all regions of this system. Explain all of your

Answer 1

E = ρ0 * r^2 * e0 /3 (r < R)

E = 0 (r > R)

Step-by-step explanation:

Using Gauss law:

`Q * e0 = \int \int E * dA`

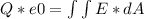
We can choose any surface to calculate the electric flux. For convenience we use a cylinder concentric to the rod. There will be no flux on the lids of the cylinder because the electric field is in the radial direction at all points.

All the points of the surface of the cylinder are at the same distance of the rod, and will have the same electric field magnitude due to symmetry.

The round surface of the cylinder is:

A = 2*π*r

Then:

Q * e0 = 2 * π * E * r

E = Q * e0 / (2 * π * r)

The electric field depends on the charge Q enclosed by the surface.

The length of the cylinder is unitary and the charge density is considered by unit of length.

Inside the rod, under the surface, the charge enclosed is:

`Q = \int\limits^(2\pi)_0 \int\limits^(R)_0 {\rho0*r} \, dr * r * d\theta`

`Q =\rho0* \int\limits^(2\pi)_0 \int\limits^(R)_0 {r^2} \, dr * d\theta`

`Q =\rho0* \int\limits^(2\pi)_0 (R^3)/(3) * d\theta`

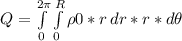
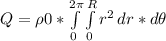
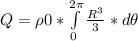
Q = ρ0 * 2/3 * π * r^3

Then:

E = ρ0 * 2/3 * π * r^3 * e0 / (2 * π * r)

E = ρ0 * r^2 * e0 /3

Outside the surface the electric field is zero because the electric charges contained in the Gauss cylinder cancel each other.

E = 0