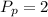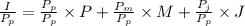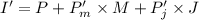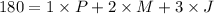Answer:
(a)
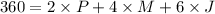
(b) 2
(c) 3
(d) 180
(e)
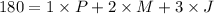
It is not different than before, he can afford the same amount of goods.
Step-by-step explanation:
let's start by writing down all the components of the problem:
1. Potato's sacs (
 ) cost 2 crowns, denote the price a potato sack by
) cost 2 crowns, denote the price a potato sack by

2. Meatballs (
 ) cost 4 per crock, denote
) cost 4 per crock, denote
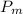 as the price of meatballs
as the price of meatballs
3. Jam cost 6 per jar (
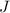 ), denote
), denote
 as the price of jam.
as the price of jam.
4. Gunnar has an Income
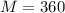
His budget constrain is then:
- The amount he spends in potatoes
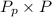
- The amount he spends in meatballs
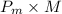
- The amount he spends in jam
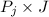
He only spends money on those goods, then his expenditures equals his income
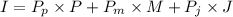
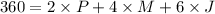
(b) Next we need to re express all prices so relative prices are the same as before.
If the new price of potatoes is
 , then the price of meatballs will be
, then the price of meatballs will be
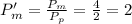
(c) the same can be done for jam
If the new price of potatoes is
 , then the price of jam will be
, then the price of jam will be
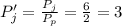
(d) Gunnar's Income would be then half as before
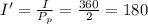
(e) We can summarize everything re expressing Gunnars budget constraint
The old budget constraint was
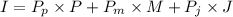
Now setting
 is the same as dividing everything by
is the same as dividing everything by