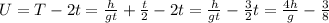Answer:
The equation for the height h(t) of an object in free fall at time t with initial velocity v₀ and initial height h₀ is given by:

The change of the height(height of the window) h with time t=0.25s:
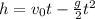
Solving for v₀, the velocity of the ball at the bottom of the window:
(i)

The equation for the velocity of an object in free fall with time T:
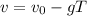
The moment the ball reaches the top of it's flight the velocity v=0:
(ii)
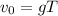
Setting equations (i) and (ii) equal and solving for T:
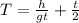
The time U it takes the ball to reappear is the difference between the flight time T and twice the time t it takes to cross the window.