Question

X+y=180
x=10y+48
(With Steps Plz)

Answer 1

(168,12)

Explanation:

Substitute x = 10y+48 in the first equation.

`10y + 48 + y = 180 \\ 11y = 180 - 48 \\ 11y = 132 \\ y = (132)/(11) \\ y = 12`

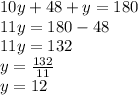
We have got the y-value. Our next goal is to find the x-value by substituting y-value in any given equations.

For me, I will be substituting y = 12 in the first equation.

`x + 12 = 180 \\ x = 180 - 12 \\ x = 168`

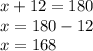
Answer Check

Substitute both x-value and y-value in both equations.

`168 + 12 = 180 \\ 180 = 180`

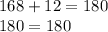
Our first equation is true for both values.

`168 = 10(12) + 48 \\ 168 = 120 + 48 \\ 168 = 168`

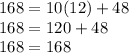
Our second equation is true for both values.

Thus, the answer is (168, 12)