Answer:
The result is

Explanation:
We have to resolve:
![[(13)/(50) +((-11))/(70)]:[((-16))/(35) .(1)/((-60)) ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/go4hjkpov0zr2xz6iz0lv2thc9hfwfxq3i.png)
First we are going to analyze by separate:
![[(13)/(50) +((-11))/(70)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nn49karhpldcsuxvgpnd6fc656nl3yavlm.png)
We have to look for the least common denominator between 50 and 70, which is 350, then we have to rewrite:
![[(13)/(50) +((-11))/(70)]=[(91)/(350)+ ((-55))/(350) ]\\\\=[(91-55)/(350) ]\\\\=[(36)/(350)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7fuxg6vm72wiamnuyf223ds1bnulcqzz7k.png)
We can simplify dividing in 2:
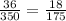
Now we have to look the other part:
![[((-16))/(35) .(1)/((-60)) ]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/astmynfbirfn71mkdo56d0nr824v6hjotn.png)
This is a multiplication so we have to cross-simplify:
We can't simplify 35 and 1 but we can simplify (-16) and (-60) in 4:
![[((-16))/(35) .(1)/((-60)) ]=[(4)/(35) .(1)/(15) ]\\\\=[(4)/(525)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/prn2v7ueuaupyea35y7ho5wnf8z4xk2n8i.png)
Now uniting what we analyzed separately:

We can simplify, we have a division then we have to simplify numerator with numerator and denominator with denominator.
We are going to simplify the numerators in 2 and the denominators in 175:

Then the result is
