Answer:
i) 90.82% of the people can complete the form in more than 5 hours
ii) The probability that the sample mean is less than 6.5 hours is 0.9986 (99.86%)
Explanation:
* Lets explain how to sole the problem
- The average time to complete a tax form is 6 hours
- Assuming the time to complete the form is normally distributed with a
standard deviation of 45 minutes
∵ 1 hour = 60 minutes
∴ 45 minutes = 45/60 = 0.75 hour
∴ The standard deviation is 0.75 hour
i)
- We need to know the percentage of the people who complete the
form in more than 5 hours
* Lets use z-score to find the probability
∵ z-score = (x - μ)/σ , where
# x is the score
# μ is the mean
# σ is the standard deviation
∵ μ = 6 , σ = 0.75 , x = 5
∴
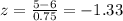
- Use the normal distribution table to find the corresponding area
of z-score -1.33
∵ The corresponding area of -1.33 = 0.09176
∵ P(x > 5) = 1 - P(z > -1.33)
∴ P(x > 5) = 1 - 0.09176 = 0.90824
- Change it to percentage by multiply it by 100%
∴ P(x > 5) = 0.90824 × 100% = 90.82%
∴ 90.82% of the people can complete the form in more than 5 hours
ii)
- A sample of 20 taxpayers are selected
- We need to know the probability that the sample mean is less
than 6.5 hours
- The sample means is called M
- The standard deviation of the distribution of sample means is
called σM where σM = σ/√n , where σ is the standard deviation and
n is the sample size
- z-score = (M - μ)/σM, where μ is the mean of the population
∵ μ = 6 , σ = 0.75 , n = 20 , M = 6.5 hours
∴ σM =
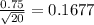
∴

- Use the normal distribution table to find the corresponding area
of z-score 2.98
∵ The corresponding area of 2.98 is 0.99856
∵ P(x < 6.5) = P(z < 2.98)
∴ P(x < 6.5) = 0.99856
∴ The probability that the sample mean is less than 6.5 hours
is 0.9986 (99.86%)