Answer:
You can determine if Tran is correct by substituting any value to "x" into each expression. If the values obtained are equal, then the expressions are equivalent.
Yes, Tran is correct (See explanation).
Explanation:
By definition, equivalent expressions havee the same value.
In this case, given the expression:
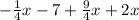
And the expression:
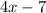
We can determine if they are equivalent by giving any value to "x", substituting into each expression and evaluate. If the values obtained are equal, then the expressions are equivalent.
To check if Tran is correct, we can give the following value to "x":

Substituting this value into the expression
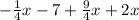 , we get:
, we get:
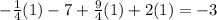
Substituting
 into the expression
into the expression
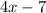 , we get:
, we get:
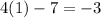
Therefore, we can conclude that Tran is correct.