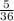Question

Two fair dice are tossed, and the up face on each die is recorded. Find the probability of observing each of the following events: A:{ The difference of the numbers is 2 or less } B:{ A 4 does not appear on either die } C:{ The sum of the numbers is 10 or more }

Answer 1

Explanation:

When two fair dice are tossed sample space consists of 36 events

(1,1)....(6,6)

A_ The difference of numbers is 2 or less

Favorable outcomes =
`(1,1) (1,2) (1,3) (2,1) (2,2)(2,3) (2,4) (3,1) (3,2) (3,3) (3,4) (3,5) (4,2) (4,3)(4,5) (4,6) (5,3) (5,4) (5,6)\\`

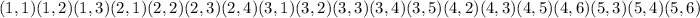
Hence Probability =
`(19)/(36)`

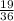
B) A 4 does not appear on either die

Then we must not have these

`(4,1)(4,2)(4,3) (4,4) (4,5) (4,6)\\(1,4) (2,4) (3,4) (5,4) (6,4)`

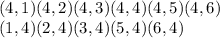
Hence probability =
`(36-11)/(36) =(25)/(36)`

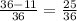
C: The sum of numbers is 10 or more:

FAvourable outcomes are:

`(4,6) (5,5) (5,6) (6,5) (6,4)`

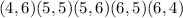
Probability =
`(5)/(36)`