Question

A shell is fired from the ground with an initial speed of 1.51 ✕ 10^3 m/s at an initial angle of 32° to the horizontal. (a) Neglecting air resistance, find the shell's horizontal range. m (b) Find the amount of time the shell is in motion.

Answer 1

(a) 209.1km

(b) 163.3sec

Step-by-step explanation:

(a) The range assuming leaving the ground is given by.

d = v2/g x sin 2 angle

d = (1.51*10^3)2/9.8 * sin 2*32..

d = 0.2091*10^6m

d = 209.1km.

(b) The horizontal component of velocity is constant and is equal to

.t = s/v

t = 0.2091*10^6/1.51*10^3*cos 32

t = 163.3sec

Answer 2

Step-by-step explanation:

Given that,

Initial speed of the shell,
`u=1.51* 10^3\ m/s`

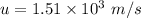
Angle of projection,
`\theta=32^(\circ)`

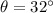
(a) The range of a projectile is given by :

`R=(u^2\ sin2\theta)/(g)`

`R=((1.51* 10^3)^2\ sin2(32))/(9.8)`

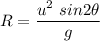
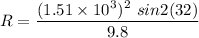
R = 209116.35 meters

(b) Let t is the amount of time the shell is in motion. It can be calculated as :

`t=(d)/(v)`

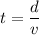
Here, d = R

`t=(R)/(u)`

`t=(209116.35\ m)/(1.51* 10^3\ m/s)`

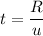
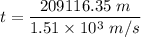
t = 138.48 seconds

Hence, this is the required solution.