Question

A square park measures 170 feet along each side. Two paved paths run from each corner to the opposite corner and extend 3 feet inwards from each corner, as shown. What is the total area, in square feet, taken by the paths?

Answer 1

The total area, in square feet, taken by the paths is 2,004

Explanation:

see the attached figure with lines to better understand the problem

I can divide the figure into four right triangles, one small square and four rectangles

step 1

Find the area of the right triangle of each corner of the path

The area of the triangle is

`A=(1/2)(b)(h)`

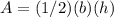
substitute the given values

`A=(1/2)(3)(3)=4.5\ ft^2`

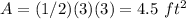
step 2

Find the hypotenuse of the right triangle

Applying Pythagoras Theorem

Let

d -----> hypotenuse of the right triangle

`d^(2)=3^(2)+3^(2)`

`d^(2)=18`

`d=√(18)\ ft`

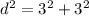
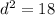
simplify

`d=3√(2)\ ft`

The hypotenuse of the right triangle is equal to the width of the path

step 2

Find the area of the small square of the path

The area is

`A=b^(2)`

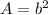
we have

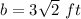`b=3√(2)\ ft` ----> the width of the path

substitute

`A=(3√(2))^(2)`

`A=18\ ft^2`

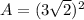
step 3

Find the length of the diagonal of the square park

Applying Pythagoras Theorem

Let

D -----> diagonal of the square park

`D^(2)=170^(2)+170^(2)`

`D^(2)=57,800`

`D=√(57,800)\ ft`

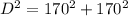
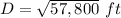
simplify

`D=170√(2)\ ft`

step 4

Find the height of each right triangle on each corner

The height will be equal to the width of the path divided by two, because is a 45-90-45 right triangle

`h=1.5√(2)\ ft`

step 5

Find the area of each rectangle of the path

The area of rectangle is
`A=LW`

we have

`W=3√(2)\ ft` ----> width of the path

Find the length of each rectangle of the path

`L=(D-2h-d)/2`

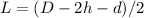
where

D is the diagonal of the park

h is the height of the right triangle in the corner

d is the width of the path (length side of the small square of the path)

substitute the values

`L=(170√(2)-2(1.5√(2))-3√(2))/2`

`L=(170√(2)-3√(2)-3√(2))/2`

`L=(164√(2))/2`

`L=82√(2)\ ft`

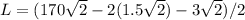
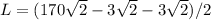
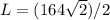
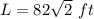
Find the area of each rectangle of the path

`A=LW`

we have

`W=3√(2)\ ft`

`L=82√(2)\ ft`

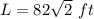
substitute

`A=(82√(2))(3√(2))`

`A=492\ ft^2`

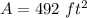
step 6

Find the area of the paths

Remember

The total area of the paths is equal to the area of four right triangles, one small square and four rectangles

so

substitute

`A=4(4.5)+18+4(492)=2,004\ ft^2`

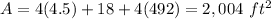
therefore

The total area, in square feet, taken by the paths is 2,004