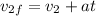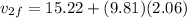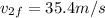Answer:
Part a)
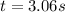
Part b)
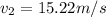
Part c)
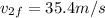
Step-by-step explanation:
Part a)
as we know that speed of the stone is 2.05 m/s
displacement of the stone is 52 m downwards
now we can use kinematics
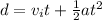

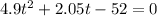
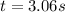
Part b)
Since second stone is projected downwards with speed v after time t = 1 s
so relative separation between two stones is given as
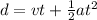
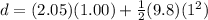
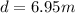
so now we can say that if both stone hit the water simultaneously so here second stone will approach 1st atone after t = 3.06 - 1 = 2.06 s
so we have
 * (2.06)= 6.95](https://img.qammunity.org/2020/formulas/physics/high-school/w98rzampeq0e0oeam13heraba6hu06udi1.png)
here v1 is the speed of first stone after t = 1 s
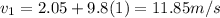
now we will have
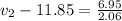
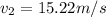
Part c)
speed of first atone when it hit the water

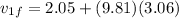
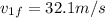
speed of 2nd stone when it will hit the water