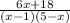Question

Give an example of a rational function (i.e., the quotient of two polynomials) f satisfying the following conditions: • f is not defined at 1. • f(−3) = 0. • f(3) = 9. • lim x→5+ f(x) = −[infinity] and lim x→5− f(x) = [infinity]. Explain your reasoning.

Answer 1

`(6x+18)/((x-1)(5-x))`

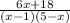
Explanation:

We have to find an example of a rational function.

Where f is satisfying the following conditions

1.f is not defined at 1.

2.f(-3)=0

3.f(3)=9

4.
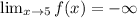
`\lim_(x\rightarrow 5) f(x)=-\infty`

5.
`\lim_(x\rightarrow)-f(x)=\infty`

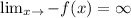
If f is not defined at 1

f has (x-1) in the denominator

`(1)/(x-1)`

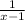
If
`\lim_(x\rightarrow)f(x)=-\infty`

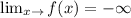
It means
`(1)/(x-5)`

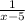
f has (5-x) in the denominator because
`(1)/(0)=\infty`

`(x-1)(5-x)=-x^2+6x-5`

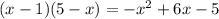
f(-3)=0

If f(-3) is zero it means numerator becomes zero when substitute x=-3 in the function

It means f has (x+3) in the numerator

f(3)=9

It means when multiply (x+3) by 6 then we get 9

because when x=3 then denominator

(3-1)(5-3)=4

When numerator is 6(x+3)

Then , substitute x=3

Then , numerator =36

After , dividing by 4 then we get 9

Therefore, we get f(3)=9

Hence,Rational function=
`(6x+18)/((x-1)(5-x))`