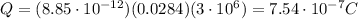Question

Students in an introductory physics lab are performing an experiment with a parallel-plate capacitor made of two circular aluminum plates, each 19 cm in diameter, separated by 1.0 cm.How much charge can be added to each of the plates before a spark jumps between the two plates? For such flat electrodes, assume that value of 3×106N/C of the field causes a spark. Express your answer with the appropriate units.

Answer 1

`7.54\cdot 10^(-7) C`

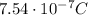
Step-by-step explanation:

The capacitance of a parallel-plate capacitor is given by

`C=(\epsilon_0 A)/(d)`

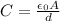
where
`\epsilon_0` is the vacuum permittivity, A is the surface area of the plates, d their separation.

We also know the following relationship

`C=(Q)/(V)`

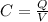
where Q is the charge stored on the capacitor and V the potential difference between the plates.

Combining the two equations,

`(\epsilon_0 A)/(d)=(Q)/(V)`

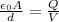
We also know that for a uniform electric field (such as the one between the plates of a parallel-plate capacitor), we have

`V= Ed`

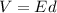
where E is the magnitude of the electric field. Substituting into the previous equation and re-arranging it,

`(\epsilon_0 A)/(d)=(Q)/(Ed)\\Q=(\epsilon_0 A E d)/(d)=\epsilon_0 A E`

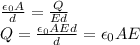
For the capacitor in the problem:

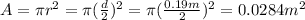`A=\pi r^2 = \pi ((d)/(2))^2 = \pi ((0.19 m)/(2))^2=0.0284 m^2` is the area of the plates

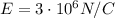`E=3\cdot 10^6 N/C` is the maximum electric field before a spark is produced

Solving for Q, we find the maximum charge that can be added before that occurs:

`Q=(8.85\cdot 10^(-12))(0.0284)(3\cdot 10^6)=7.54\cdot 10^(-7) C`