Question

Jeffrey calculated the slope between two pairs of points. He found that the slope between -5, 6 and -3, 2 is -2. He also found that the slope between (-1, -2) and (0, -4) is -2. Jeffrey concluded that all of these points are on the same line. Use the drop-down menus to complete the statements about Jeffrey's conclusion. Jeffrey is (correct/incorrect). All of these points (are/are not) on the same line because the slope between(-3,2) and( 0,-4), which are coordinates from each of the pairs above,(is/is not) equal to -2.

Answer 1

Answeit is correct, are, and is

Explanation:

Answer 2

Jeffrey is correct

All of these points are on the same line because the slope between (-3,2) and( 0,-4), which are coordinates from each of the pairs above, is equal to -2

Explanation:

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

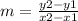
step 1

Find the slope between -5, 6 and -3, 2

substitute the values in the formula

`m=(2-6)/(-3+5)`

`m=(-4)/(2)=-2`

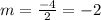
step 2

Find the slope between (-1, -2) and (0, -4)

substitute the values in the formula

`m=(-4+2)/(0+1)`

`m=(-2)/(1)=-2`

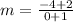
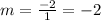
step 3

Find the slope between (-3, 2) and (0, -4)

substitute the values in the formula

`m=(-4-2)/(0+3)`

`m=(-6)/(3)=-2`

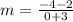
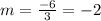
therefore

Jeffrey is correct

All of these points are on the same line because the slope between (-3,2) and( 0,-4), which are coordinates from each of the pairs above, is equal to -2