Question

Consider a right-angled triangle (i.e., a triangle in which one of the angles is 90degrees). If the two sides that form the 90 degree corner are 4 inches and 3 inches, then the area of the triangle is equal to what? [Hint: Draw that triangle and relate it to a rectangle].

Answer 1

The area of the triangle is equal to 6 square inches.

Explanation:

Following the hint and drawing the right-angled triangle related to a rectangle, you get the drawing attached at the bottom of this answer.

As you can see in the drawing, the right-angled triangle is the perfect half of the resulting rectangle, so in order to calculate the area of the triangle, you can calculate the area of the rectangle and then divide it by 2.

The area of the rectangle is obtained by multiplying its length by its width, which in this case are 4 in and 3 in, respectively:

Rectangle area = Length x width = 4 in x 3 in = 12 sq in

Since we stablished that the area of the triangle is half the area of the rectangle, we get:

Triangle area =
`(12 sq in)/(2) = 6 sq in`

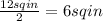
So the area of the triangle is 6 square inches.