Question

After being assaulted by flying cannonballs, the knights on the castle walls (12 m above the ground) respond by propelling flaming pitch balls at their assailants. One ball lands on the ground at a distance of 50 m from the castle walls. If it was launched at an angle of 53° above the horizontal, what was its initial speed?

Answer 1

The answer is 24,9 mts/seg

Step-by-step explanation:

The attachment shows a schematic of the situation.

Due we don't have the flying time of the projectile, we can use, From the projectile motion equations the next expression:

`y = x tan\alpha - (g x^(2))/(2 Vo^(2) cos\alpha)`

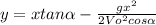
Where:

y is the altitude of the wall

x is the distance from the wall where the ball landed

`\alpha` is the shoot angle

Vo is the initial velocity

Clearing Vo, we obtain:

Vo =
`\sqrt{(g x^(2))/(2 cos^(2)\alpha(x tan\alpha - y))}`

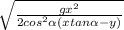
Knowing that y = 12 mts; x = 50 mts and
`\alpha` = 53° and gravity constant is 9.8 mts/seg2; the only thing that we must do is replace the values on the formula:

Vo =
`Vo = \sqrt{((9.8)(50^(2)))/(2cos^(2)53(50tan53-12))}`

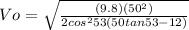
Vo = 24,9 mts/seg