Answer:
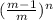
Explanation:
Given a basket, the probability of a ball to end there is
 (because there are m baskets).
(because there are m baskets).
Then, the probability of a ball to end in other basket is
 .
.
Finally, the probability of the basket to remain empty after n throws is
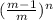
This last is because, given n independets events with probability p, the probability for all of them to happen is
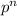 . In this case
. In this case
