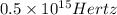Question

Given that the energy difference between the ground state and the first excited electronic state (E) for the sodium atom is 3.373 × 10-19 J, calculate the frequency, , corresponding to a photon possessing this energy. Next, calculate the wavelength (in nm) for this photon.

Answer 1

Answer: Frequency corresponding to a photon possessing this energy is
`0.5* 10^(15)Hertz`

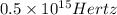
Wavelength for this photon is 600 nm.

Step-by-step explanation:

The relationship between wavelength and energy of the wave follows the equation:

`E=(hc)/(\lambda)`

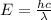
E= energy

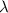`\lambda` = wavelength of the wave

h = Planck's constant =
`6.626* 10^(-34)Js`

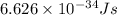
c = speed of light =
`3* 10^8m/s`

`3.373* 10^(-19)=(6.626* 10^(-34)* 3* 10^8m/s)/(\lambda)`

`\lambda=6* 10^(-7)m=600nm`
`1m=10^9nm`

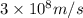
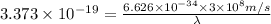
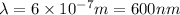
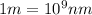
Thus wavelength for this photon is 600 nm.

The relationship between wavelength and frequency of the wave follows the equation:

`\\u=(c)/(\lambda)`

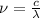
where,

`\\u` = frequency of the wave

c = speed of light

`\\u=(3* 10^8m/s)/(6* 10^(-7)m)`

`\\u=0.5* 10^(15)s^(-1)=0.5* 10^(15)Hertz`

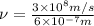
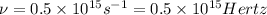
Thus frequency corresponding to a photon possessing this energy is
`0.5* 10^(15)Hertz`