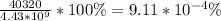Question

Eight rooks are placed randomly on a chess board. What is the probability that none of the rooks can capture any of the other rooks? Translation for those unfamiliar with chess: 8 unit squares are chosen uniformly at random from an 8x8 grid, no 2 overlapping. What is the probability that no two chosen squares share a row or a column?

Answer 1

9.11*10^-4 %

Explanation:

To find the probability, you simply need to find the possible outcomes that allows no rooks to be in danger, and the possible amount of ways to place the rooks.

For the first outcome, you start by putting 1 rook in the first columns, you have 8 possible rows to do this. The next rook in the next column will only have 7 possible rows, as you have to exclude the one where the previous rook is located. The next rook, 6 possibilities, the next 5, and so on. So we conclude that the total amount of ways so that none of the rooks can capture any of the other rooks is 8*7*6*5*4*3*2*1 = 8! = 40320

In order to find the total amount of ways to place the rooks, you can just use a combinatoric:

`\left[\begin{array}{ccc}64\\8\end{array}\right]= (64!)/(8!(64-8)!) = 4.43*10^9`

Then:

P =
`(40320)/(4.43*10^9)*100\%=9.11*10^(-4)\%`