Answer:
∅=10.7°
Step-by-step explanation:
In parabolic motion the position on the x-axis can be found like this.
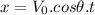
Where we clear the time.
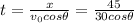
The position on the y-axis can be found as well.
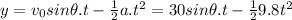
replacing time.
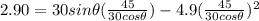
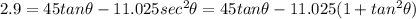
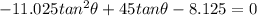
Now we use the quadratic equation to find the tangent of the angle.
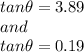
Finally we use the arc tangent function to find the angle.
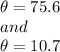
We choose the second angle because it adapts to the situation described, that is the minimum angle.