Step-by-step explanation:
Given that,
Angular frequency 1,
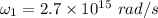
Angular frequency 2,

When light having vibrations with angular frequency ranging from
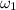 to
to
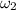 strikes the retina of the eye, it stimulates the receptor cells there and is perceived as visible light. We need to find the limits of the period of this light.
strikes the retina of the eye, it stimulates the receptor cells there and is perceived as visible light. We need to find the limits of the period of this light.
We know that,
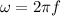
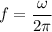
Time period,
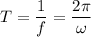
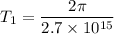
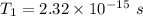
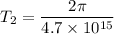
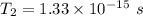
So, the limits of the period of this light is from
 to
to
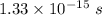 . Hence, this is the required solution.
. Hence, this is the required solution.