Answer:
3 in each case.
Step-by-step explanation:
We've got the position function
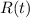 . We can see that it's the equation of a line. That is, if we were to graph the position R against the time t, we would get a line.
. We can see that it's the equation of a line. That is, if we were to graph the position R against the time t, we would get a line.
On the other hand, the velocity is the rate of change of the position related to the time. Since the position is a lineal function, we can calculate the speed taking
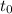 as the starting moment and
as the starting moment and
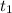 as the end moment measure the distance travelled. The distance travelled from instant 0 to instant 1 would the be
as the end moment measure the distance travelled. The distance travelled from instant 0 to instant 1 would the be
 and the time spend in that time would be
and the time spend in that time would be
 . So the velocity v is:
. So the velocity v is:
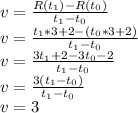
So we get that the velocity is the same for whichever two points we use to calculate it. Hence, it's constant and it's value is 3, so the average is also the same no matter the time we use.
The units are not shown here because the question doesn't say which are used, but in the metric system it's meters/seconds.