Question

A ball is dropped from the top of a building that is known to be 400 feet high. The formula for finding the height of the ball at any time is h=400−16t2, where t is measured in seconds.

How many seconds did it take for the ball to reach a height of 256 feet above the ground?

Answer 1

3 seconds

Step-by-step explanation:

Height of the building = 400 feet

Height of the ball from the ground is given by

h=400−16t²

This formula has been derived from

`s=ut+(1)/(2)at^2`

a = Acceleration due to gravity = 32 ft/s²

u = Initial velocity = 0

t = Time taken

Substituting all the values we get

`s=0t+(1)/(2)32t^2\\\Rightarrow s=16t^2`

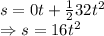
This is the height of the ball from the top of the building

The height of the ball from the ground will be

h = 400-s

⇒h = 400−16t²

When h = 256 ft

`256=400-16t^2\\\Rightarrow t=\sqrt{(256-400)/(-16)}\\\Rightarrow t=3\ s`

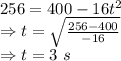
Time taken by the ball to reach a height of 256 feet above the ground is 3 seconds