Answer:
The average velocity of an object is defined as the total displacement covered by the particle divided by the total time taken in covering that displacement.
Let the position of the particle at any time t be
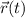 .
.
Position of the particle at time
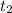 =
=
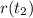 .
.
Position of the particle at time
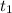 =
=
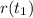 .
.
Total displacement covered by the particle in time from
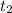 to
to
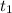 =
=

Therefore, the average velocity is given by

Now, the instantaneous velocity is defined as
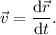
The average value of instantaneous velocity in the same time interval is given by
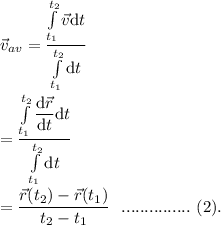
Thus, from (1) and (2), it is clear that the average velocity of a particle calculated for the time interval from t1 to t2 really is the average value of the particle’s instantaneous velocity
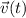 over the same time interval.
over the same time interval.