Question

Let S(n)=1+2+···+ n be the sum of the first n natural numbers and let C(n)=1 3 +2 3 + ···+ n3 be the sum of the first n cubes. Prove the following equalitiesby inductionon n, to arriveat thecurious conclusionthatC(n)=S2(n) for every

Answer 1

Explanation:

We have

`S_n =(n(n+1))/(2) \\C_n = ((n(n+1))/(2))^2`

To prove that
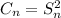`C_n = S_n^2` by induction

Let P(n) be that statement for n

n=1 gives left side =1 =right side

True for n=1

Assume that P(k) is true

i.e.
`S_k^2 = C_k`

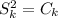
We have to prove P(k+1) is true assuming P(k)

LHS of
`P(k+1) = (((k+1)(k+2))/(2) )^2`

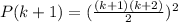
RHS =
`C_k+(k+1)^3\\= ((k(k+1))/(2) )^2+(k+1)^3`

since by adding last term with Ck gives the sum

For simplification take (k+1) square outside

RHS =
`((k+1)^2)/(4) [k^2+4(k+1)]\\=((k+1)^2)/(4)(k+2)^2\\=LHS`

Thus proved by mathematical induction