Answer:0.0869 %
Step-by-step explanation:
Given
probability of getting success is 50 % i.e. 0.5
So probability of missing the throw is 0.5
For 20 shots probability that he can score five baskets
Using Binomial distribution
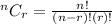
here n=20
p=0.5 (Probability of winning)
q=0.5 (Probability of loosing)
for r=5
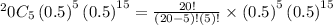
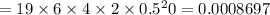
i.e. 0.0869 %