Question

Give an example of a point that is the same distance from (3, 0) as it is from (7, 0). Find lots of examples. Describe the configuration of all such points. In particular, how does this configuration relate to the two given points?

Answer 1

Supposse that the distance from the point
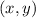`(x,y)` to the point
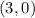`(3,0)` is equal to the distance from
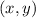`(x,y)` to the point
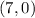`(7,0)`. Then, by the formula of the distnace we must have

`√((x-3)^2 + (y-0)^2)=√((x-7)^2 + (y-0)^2)`

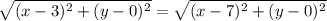
cancel the square root and the
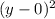`(y-0)^2`'s, and then expand the parenthesis to obtain

`x^2 - 6x + 9 = x^2 - 14x + 49`

then, simplifying we obtain

`8x = 40`

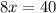
therfore we must have

`x=5`

this means that the points satisfying the propertie must have first component equal to 5. So we can give a lot of examples of such points:
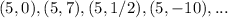`(5,0), (5,7),(5,1/2), (5,-10),...`. The set of this points give us a straight line and the points (3,0) and (7,0) are symmetric with respect to this line.