Answer:
19554575040
Step-by-step explanation:
The first five positions to be named as Grand Prize winners are not give any order.
Therefore, the number of ways they can be selected is
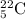
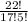
Now the remaining 5 positions are selected from the remaining 17 entries. So they can be ordered as,
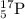
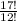
17 x 16 x 15 x 14 x 13 ways of ordering
Therefore, the number of ways in which the entries can be announced is
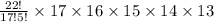
= 19554575040 number of ways
Thus the announcement can be made in 19554575040 number of ways.