Question

Write the differential equation model that fits the given description. (a) The rate of change of the volume of a snowball (due to melting) is proportional to the square of the volume at time t. Initially, the snowball has a volume of 900 cm3 . (b) For an insect moving along some path, the velocity at time t is proportional to the square root of its position.

Answer 1

a) he rate of change of the volume of a snowball (due to melting) is proportional to the square of the volume at time t. Initially, the snowball has a volume of 900 cm3

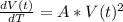`(dV(t))/(dT) = A*V(t)^(2) \\` and V(0) = 900
`cm^(3)`

where A is a real constant, it appears because it says that the change i volume (dV/dt) is "proportional" to
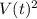`V(t)^(2)`. Furthermore, we should assume that A is a negative number, because the volume of the snowball will decrease as the time pasese by.

(b) For an insect moving along some path, the velocity at time t is proportional to the square root of its position.

`(dr(t))/(dt)  = B*√(r(t))`

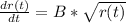
Here again appears a constant B for the "proportional" part. And i wrote the velocity as
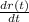`(dr(t))/(dt)` "the rate of change of the position with respect to te time".