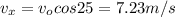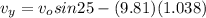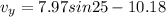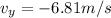Answer:
time after which it will hit the floor
t = 1.038 s
initial speed is given as
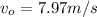
final component of velocities
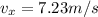
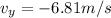
Step-by-step explanation:
Height of the water balloon from which it is projected is given as
h = 1.78 m
now we know that
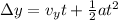

also we know that
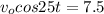
now we have
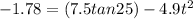
now we have
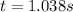
Now we have
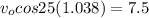
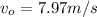
Now final speed when it hit the floor in x and y direction is given as