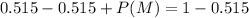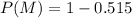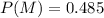Answer:
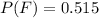
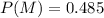
Step-by-step explanation:
Given
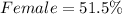
Solving (a): Probability of running into a female
To do this, we simply convert the given proportion to decimal
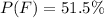
Convert to fraction
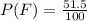
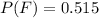
Solving (b): Probability of running into a male
Represent this with
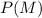
To solve this, we apply the concept of probability complement which states that:
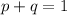
In this case:

Substitute 0.515 for P(F)
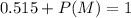
Subtract 0.515 from both sides