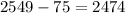Question

A pilot sample of 75 items was​ taken, and the number of items with the attribute of interest was found to be 30. How many more items must be sampled to construct a 99​% confidence interval estimate for p with a 0.025 margin of​ error?

Answer 1

Answer: 2474

Explanation:

Given : A pilot sample of 75 items was​ taken, and the number of items with the attribute of interest was found to be 30.

Then, prior estimate for proportion of attribute of interest:
`p=(30)/(75)=0.4`

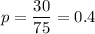
Significance level :
`\alpha: 1-0.99=0.01`

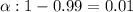
Critical value :
`z_(\alpha/2)=2.576`

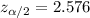
Margin of error :
`E=0.025`

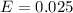
The formula use to find the sample size :_

`n=p(1-p)((z_(\alph/2))/(E))^2\\\\\Rightarrow\ n=(0.4)(1-0.4)((2.576)/(0.025))`

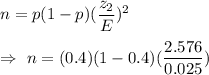
Now, simplify , we get

`n=2548.137984\approx2549`

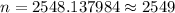
Now, the number of items more to sample =
`2549-75=2474`